Problem

Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must appear as many times as it shows in both arrays and you may return the result in any order.

Example 1:

Input: nums1 = [1,2,2,1], nums2 = [2,2]
Output: [2,2]

Example 2:

Input: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
Output: [4,9]
Explanation: [9,4] is also accepted.

Constraints:

• 1 <= nums1.length, nums2.length <= 1000
• 0 <= nums1[i], nums2[i] <= 1000

Follow-up:

• What if the given array is already sorted? How would you optimize your algorithm?
• What if nums1’s size is small compared to nums2’s size? Which algorithm is better?
• What if elements of nums2 are stored on disk, and the memory is limited such that you cannot load all elements into the memory at once?

---

Approach & Explanation

There are two main approaches to solve this problem:

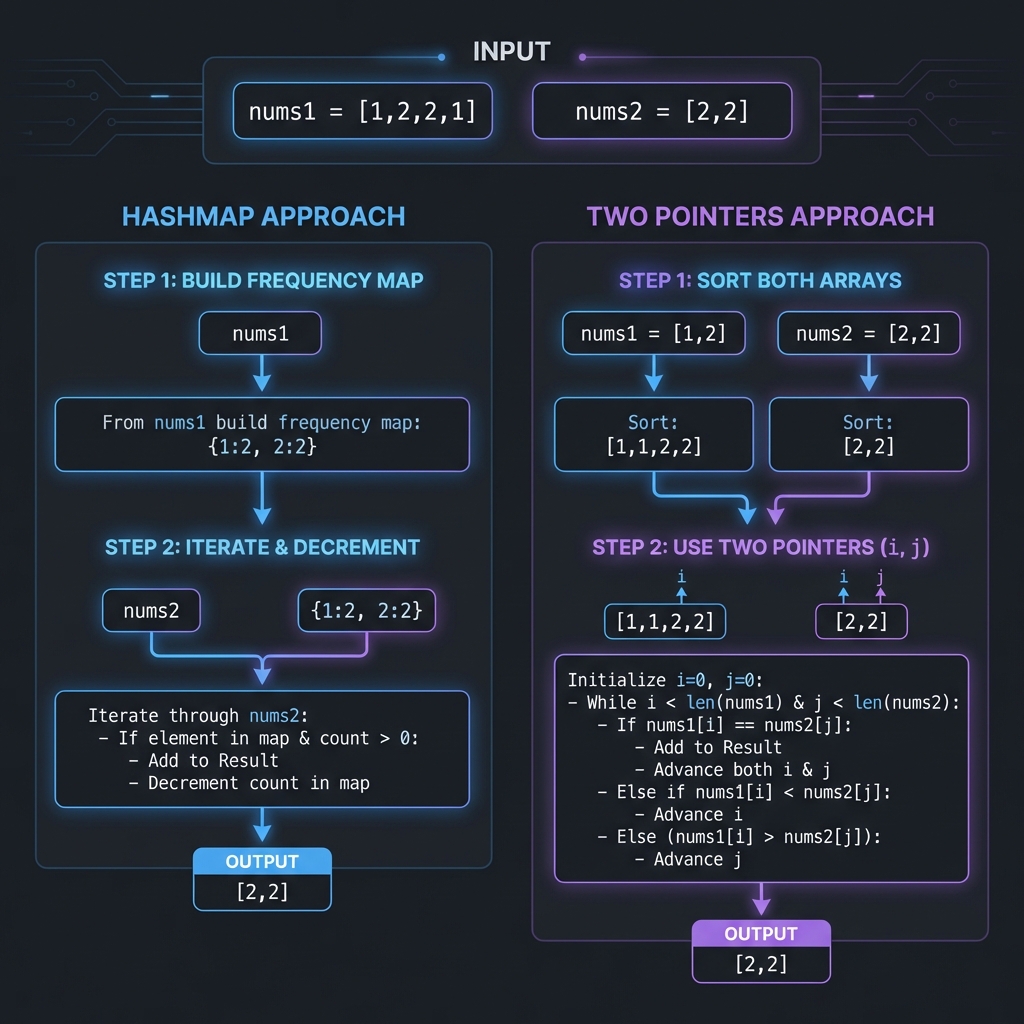
Approach 1: HashMap (Frequency Count)

1. Swap arrays so nums1 is always the larger array (for in-place result storage)
2. Build a frequency map from nums1
3. Iterate through the smaller array (nums2)
4. If element exists in map with count > 0, add to result and decrement count

Note: Some implementations build the map from the smaller array for space optimization. This implementation builds from the larger array to allow reusing nums1 for the output.

Complexity:

• Time: O(m + n)
• Space: O(max(m, n)) for the hashmap

Approach 2: Two Pointers (Sorted Arrays)

1. Sort both arrays
2. Use two pointers, one for each array
3. If elements are equal, add to result and advance both pointers
4. Otherwise, advance the pointer with the smaller element

Complexity:

• Time: O(m log m + n log n) due to sorting
• Space: O(1) if we ignore the output array

When to Use Which?

Scenario	Best Approach
Arrays already sorted	Two Pointers
One array much smaller	HashMap (on smaller array)
Memory limited	Two Pointers (external sort)
General case	HashMap

---

Solution

Approach 1: HashMap

Java

import java.util.Map;
import java.util.HashMap;
import java.util.Arrays;

class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        if(nums1.length < nums2.length) {
            return intersect(nums2, nums1);
        }
        Map<Integer, Integer> count = new HashMap<>();

        for (int num : nums1) {
            count.merge(num, 1, Integer::sum);
        }
        int k = 0;
        for(int num : nums2) {
            int cnt = count.getOrDefault(num, 0);
            if(cnt > 0) {
                nums1[k++] = num;
                count.merge(num, -1, Integer::sum);
            }
        }

        return Arrays.copyOfRange(nums1, 0, k);
    }
}

Go

func intersect(nums1 []int, nums2 []int) []int {
    if len(nums1) < len(nums2) {
        return intersect(nums2, nums1)
    }

    count := make(map[int]int)

    for _, num := range nums1 {
        count[num]++
    }

    k := 0

    for _, num := range nums2 {
        if count[num] > 0 {
            count[num]--
            nums1[k] = num
            k++
        }
    }

    return nums1[:k]
}

---

Approach 2: Two Pointers

Java

import java.util.Arrays;

class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        Arrays.sort(nums1);
        Arrays.sort(nums2);

        int i = 0, j = 0, k = 0;
        while(i < nums1.length && j < nums2.length) {
            if(nums1[i] == nums2[j]) {
                nums1[k++] = nums1[i];
                i++;
                j++;
            } else if (nums1[i] < nums2[j]) {
                i++;
            } else {
                j++;
            }
        }

        return Arrays.copyOfRange(nums1, 0, k);
    }
}

Go

import "sort"

func intersect(nums1 []int, nums2 []int) []int {
    sort.Ints(nums1)
    sort.Ints(nums2)

    var intersection []int

    for i, j := 0, 0; i < len(nums1) && j < len(nums2); {
        if nums1[i] == nums2[j] {
            intersection = append(intersection, nums1[i])
            i++
            j++
        } else if nums1[i] < nums2[j] {
            i++
        } else {
            j++
        }
    }

    return intersection
}

---

Key Insight

The HashMap approach is generally preferred because it has better time complexity (O(m+n) vs O(m log m + n log n)). However, if the arrays are already sorted or if memory is extremely limited, the Two Pointers approach becomes more efficient.